Fuzzing: Breaking Things with Random Inputs¶
In this chapter, we'll start with one of the simplest test generation techniques. The key idea of random text generation, also known as fuzzing, is to feed a string of random characters into a program in the hope to uncover failures.
from typing import Dict, Tuple, Union, List, Any
Now, we explicitly import (and thus require) the earlier chapter.
A Testing Assignment¶
Fuzzing was born in a "dark and stormy night in the Fall of 1988" \cite{Takanen2008}. Sitting in his apartment in Wisconsin, Madison, professor Barton Miller was connected to his university computer via a 1200 baud telephone line. The thunderstorm caused noise on the line, and this noise in turn caused the UNIX commands on either end to get bad inputs – and crash. The frequent crashes surprised him – surely, programs should be more robust than that? As a scientist, he wanted to investigate the extent of the problem and its causes. So he crafted a programming exercise for his students at the University of Wisconsin-Madison – an exercise that would have his students create the first fuzzers.
This is how the assignment read:
The goal of this project is to evaluate the robustness of various UNIX utility programs, given an unpredictable input stream. [...] First, you will build a fuzz generator. This is a program that will output a random character stream. Second, you will take the fuzz generator and use it to attack as many UNIX utilities as possible, with the goal of trying to break them.
This assignment captures the essence of fuzzing: Create random inputs, and see if they break things. Just let it run long enough, and you'll see.
A Simple Fuzzer¶
Let us try to fulfill this assignment and build a fuzz generator. The idea is to produce random characters, adding them to a buffer string variable (out), and finally returning the string.
This implementation uses the following Python features and functions:
random.randrange(start, end)– return a random number $[$start,end$)$range(start, end)– create an iterator (which can be used as a list) with integers in the range $[$start,end$)$.for elem in list: body– executebodyin a loop withelemtaking each value fromlist.for i in range(start, end): body– executebodyin a loop withifromstarttoend$-$ 1.chr(n)– return a character with ASCII coden
def fuzzer(max_length: int = 100, char_start: int = 32, char_range: int = 32) -> str:
"""A string of up to `max_length` characters
in the range [`char_start`, `char_start` + `char_range`)"""
string_length = random.randrange(0, max_length + 1)
out = ""
for i in range(0, string_length):
out += chr(random.randrange(char_start, char_start + char_range))
return out
With its default arguments, the fuzzer() function returns a string of random characters:
fuzzer()
'!7#%"*#0=)$;%6*;>638:*>80"=</>(/*:-(2<4 !:5*6856&?""11<7+%<%7,4.8,*+&,,$,."'
Bart Miller coined the term "fuzz" as the name for such random, unstructured data. Now imagine that this "fuzz" string was the input to a program expecting a specific input format – say, a comma-separated list of values, or an e-mail address. Would the program be able to process such an input without any problems?
If the above fuzzing input already is intriguing, consider that fuzzing can easily be set up to produce other kinds of input. For instance, we can also have fuzzer() produce a series of lowercase letters. We use ord(c) to return the ASCII code of the character c.
fuzzer(1000, ord('a'), 26)
'zskscocrxllosagkvaszlngpysurezehvcqcghygphnhonehczraznkibltfmocxddoxcmrvatcleysksodzlwmzdndoxrjfqigjhqjxkblyrtoaydlwwisrvxtxsejhfbnforvlfisojqaktcxpmjqsfsycisoexjctydzxzzutukdztxvdpqbjuqmsectwjvylvbixzfmqiabdnihqagsvlyxwxxconminadcaqjdzcnzfjlwccyudmdfceiepwvyggepjxoeqaqbjzvmjdlebxqvehkmlevoofjlilegieeihmetjappbisqgrjhglzgffqrdqcwfmmwqecxlqfpvgtvcddvmwkplmwadgiyckrfjddxnegvmxravaunzwhpfpyzuyyavwwtgykwfszasvlbwojetvcygectelwkputfczgsfsbclnkzzcjfywitooygjwqujseflqyvqgyzpvknddzemkegrjjrshbouqxcmixnqhgsgdwgzwzmgzfajymbcfezqxndbmzwnxjeevgtpjtcwgbzptozflrwvuopohbvpmpaifnyyfvbzzdsdlznusarkmmtazptbjbqdkrsnrpgdffemnpehoapiiudokczwrvpsonybfpaeyorrgjdmgvkvupdtkrequicexqkoikygepawmwsdcrhivoegynnhodfhryeqbebtbqnwhogdfrsrksntqjbocvislhgrgchkhpaiugpbdygwkhrtyniufabdnqhtnwreiascfvmuhettfpbowbjadfxnbtzhobnxsnf'
Assume a program expects an identifier as its input. Would it expect such a long identifier?
quiz("Which of these produces strings with arbitrary long decimal numbers?",
[
"`fuzzer(100, 1, 100)`",
"`fuzzer(100, 100, 0)`",
"`fuzzer(100, 10, ord('0'))`",
"`fuzzer(100, ord('0'), 10)`",
], "1 ** (2 % 3) * 4")
Quiz
Indeed! It is the last one that does the trick:
fuzzer(100, ord('0'), 10)
'905902398493166953126081485047020401153418590518545517740565959745145909835837'
Fuzzing External Programs¶
Let us see what happens if we actually invoke an external program with fuzzed inputs. To this end, let us proceed in two steps. First, we create an input file with fuzzed test data; then we feed this input file into a program of choice.
Creating Input Files¶
Let us obtain a temporary file name such that we do not clutter the file system.
basename = "input.txt"
tempdir = tempfile.mkdtemp()
FILE = os.path.join(tempdir, basename)
print(FILE)
/var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt
We can now open this file for writing. The Python open() function opens a file into which we can then write arbitrary contents. It is commonly used in conjunction with the with statement, which ensures that the file is closed as soon as it is no longer needed.
data = fuzzer()
with open(FILE, "w") as f:
f.write(data)
We can verify that the file was actually created by reading its contents:
contents = open(FILE).read()
print(contents)
assert(contents == data)
<?6&" !3'7-5>18%55*,5
Invoking External Programs¶
Now that we have an input file, we can invoke a program on it. For the fun of it, let us test the bc calculator program, which takes an arithmetic expression and evaluates it.
To invoke bc, let us use the Python subprocess module. This is how this works:
import os
import subprocess
program = "bc"
with open(FILE, "w") as f:
f.write("2 + 2\n")
result = subprocess.run([program, FILE],
stdin=subprocess.DEVNULL,
stdout=subprocess.PIPE,
stderr=subprocess.PIPE,
universal_newlines=True) # Will be "text" in Python 3.7
From the result, we can check the program output. In the case of bc, this is the result of evaluating the arithmetic expression:
result.stdout
'4\n'
We can also check the status. A value of 0 indicates that the program terminated correctly.
result.returncode
0
Any error messages would be available in results.stderr:
result.stderr
''
Instead of bc, you can actually put in any program you like. Be aware, though, that if your program is able to change or even damage your system, there is quite a risk that the fuzzed input contains data or commands that do precisely this.
quiz("Just for the fun of it, imagine you would test a file removal program - "
"say `rm -fr FILE`, where `FILE` is a string produced by `fuzzer()`. "
"What is the chance of `fuzzer()` (with default arguments) producing a `FILE` "
"argument that results in deleting all your files?",
[
"About one in a billion",
"About one in a million",
"About one in a thousand",
"About one in ten"
], "9 ** 0.5")
Quiz
rm -fr FILE, where FILE is a string produced by fuzzer(). What is the chance of fuzzer() (with default arguments) producing a FILE argument that results in deleting all your files?
The chance is actually higher than you may think. If you remove / (the root of all files), for instance, your entire file system will be gone. If you remove . (the current folder), all the files in the current directory will be gone.
The probability of generating a string that is exactly 1 character long is 1/101, this is because the length of the string is determined by calling random.randrange(0, max_length + 1), where the default value of max_length is 100. Per the description given of random.randrange, that should return a random number in [0, 99 + 1). So, we end up with the inclusive range [0, 100] where there are 101 values in the interval.
For / or . to be produced, you need a string length of 1 (chance: 1 out of 101) and one of these two characters (chance: 2 out of 32).
1/101 * 2/32
0.0006188118811881188
The above code block precludes the possibility of removing ~ (your home directory), this is because the probability of generating the character '~' is not 1/32; it is 0/32. The characters are created by calling chr(random.randrange(char_start, char_start + char_range)), where the default value of char_start is 32 and the default value of char_range is 32. The documentation for chr reads, "[r]eturn the string representing a character whose Unicode code point is the integer i." The Unicode code point for '~' is 126 and therefore, not in the interval [32, 64).
If the code were to be changed so that char_range = 95 then the probability of obtaining the character '~' would be 1/94 , thus resulting in the probability of the event of deleting all files being equal to 0.000332
And all your files in the home directory will be gone
3/94 * 1/94 * 99/101
0.0003327969736765437
However, we can actually deal with any string as long as the second character is a space – after all, rm -fr / WHATEVER will first deal with /, and only then with whatever follows. The chances for the first character are 2 out of 32 as the code block above only allows for the probability of obtaining a / or a . but not a ~.
For the space the probability is 1 out of 32.
We have to include the term for the probability of obtaining at least 2 characters which is required for the scenario of obtaining a space as the second character. This probability is 99/101 because it is calculated as (1 - probability of obtaining a single character or no character at all), so it is equal to 1-(2/101).
Therefore, the probability calculation for the event of deleting all files in the case of having a space for the second character is:
[probability of obtaining '/' or '. ' followed by a space] = [the probability of obtaining either the '/' character or the '. ' character] * [the probability of obtaining space] * [Probability of getting at least 2 characters] = 0.001914
Diagram of probability of obtaining at least 2 characters.
2/32 * 1/32 * 99/101
0.0019144492574257425
Given that fuzz tests are typically run millions of times, you really don't want to take this risk. Run your fuzzers in a safe environment that you can reset at will, such as a Docker container.
Long-Running Fuzzing¶
Let us now feed a large number of inputs into our tested program, to see whether it might crash on some. We store all results in the runs variable as pairs of input data and the actual result. (Note: running this may take a while.)
trials = 100
program = "bc"
runs = []
for i in range(trials):
data = fuzzer()
with open(FILE, "w") as f:
f.write(data)
result = subprocess.run([program, FILE],
stdin=subprocess.DEVNULL,
stdout=subprocess.PIPE,
stderr=subprocess.PIPE,
universal_newlines=True)
runs.append((data, result))
We can now query runs for some statistics. For instance, we can query how many runs actually passed -- that is, there were no error messages. We use a list comprehension here: The form expression for element in list if condition returns a list of evaluated expressions in which each element comes from list if the condition was true. (Actually, a list comprehension returns a list generator, but for our purposes, the generator behaves like a list.) Here, we have the expression be 1 for all elements where condition holds, and we use sum() to sum over all elements in the list.
sum(1 for (data, result) in runs if result.stderr == "")
9
Most inputs apparently are invalid – not a big surprise, as it is unlikely that a random input contains a valid arithmetic expression.
Let us take a look at the first error message:
errors = [(data, result) for (data, result) in runs if result.stderr != ""]
(first_data, first_result) = errors[0]
print(repr(first_data))
print(first_result.stderr)
'5&8>"86,?"/7!1%5-**&-$&)$91;"21(\'8"(%$4,("(&!67%89$!.?(*(96(28$=6029:<:$(6 !-+2622(&4'
Parse error: bad character '&'
/var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1
Are there any runs with messages other than illegal character, parse error, or syntax error? (Say, something like crash or you found a fatal bug?) Not very many:
[result.stderr for (data, result) in runs if
result.stderr != ""
and "illegal character" not in result.stderr
and "parse error" not in result.stderr
and "syntax error" not in result.stderr]
["\nParse error: bad character '&'\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n", '\nParse error: bad expression\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad expression\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad token\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad token\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad token\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad token\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad token\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad expression\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad token\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad token\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad expression\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad expression\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad expression\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad expression\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad token\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad expression\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', "\nParse error: bad character '&'\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n", '\nParse error: bad assignment: left side must be scale, ibase, obase, seed, last, var, or array element\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad expression\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', "\nParse error: bad character '?'\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n", "\nParse error: bad character '''\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n", '\nParse error: bad token\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', "\nParse error: bad character '?'\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n", "\nParse error: bad character ':'\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n", "\nParse error: bad character '&'\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n", "\nParse error: bad character ':'\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n", '\nParse error: bad token\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad token\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad expression\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', "\nParse error: bad character '?'\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n", '\nParse error: bad assignment: left side must be scale, ibase, obase, seed, last, var, or array element\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad token\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad expression\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad token\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', "\nParse error: bad character '&'\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n", "\nParse error: bad character '''\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n", '\nParse error: bad token\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad expression\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', "\nParse error: bad character '''\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n", "\nParse error: bad character '''\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n", "\nParse error: bad character '&'\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n", '\nParse error: bad token\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad token\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', "\nParse error: bad character ':'\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n", "\nParse error: bad character ':'\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n", '\nParse error: bad expression\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad expression\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad token\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', "\nParse error: bad character '&'\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n", '\nParse error: bad token\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad expression\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad expression\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad token\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad expression\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', "\nParse error: bad character ':'\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n", "\nParse error: bad character ':'\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n", '\nParse error: bad expression\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad token\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad token\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad token\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad expression\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad expression\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', "\nParse error: bad character '&'\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n", "\nParse error: bad character '&'\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n", "\nParse error: bad character '''\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n", '\nParse error: bad token\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad expression\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', "\nParse error: bad character ':'\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n", '\nParse error: bad expression\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', "\nParse error: bad character '''\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n", '\nParse error: bad expression\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', "\nParse error: bad character ':'\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n", "\nParse error: bad character '''\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n", '\nParse error: bad token\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad token\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad token\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad expression\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad token\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', "\nParse error: bad character '&'\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n", '\nParse error: bad token\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad token\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', "\nParse error: bad character '?'\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n", '\nParse error: bad expression\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad expression\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad expression\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', "\nParse error: bad character ':'\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n", "\nParse error: bad character '''\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n", '\nParse error: bad expression\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad token\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n', '\nParse error: bad token\n /var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/tmptur5lzbo/input.txt:1\n\n']
Maybe a crash would be indicated by bc just crashing. Unfortunately, the return code is never nonzero:
sum(1 for (data, result) in runs if result.returncode != 0)
91
How about we let the above bc test run for some more? While it is running, let us take a look on how the state of the art was in 1989.
Bugs Fuzzers Find¶
When Miller and his students ran their first fuzzers in 1989, they found an alarming result: About a third of the UNIX utilities they fuzzed had issues – they crashed, hung, or otherwise failed when confronted with fuzzing input \cite{Miller1990}. This also included the bc program, above. (The bc above is a modern reimplementation whose author is a staunch believer in fuzzing!)
Considering that many of these UNIX utilities were used in scripts that would also process network input, this was an alarming result. Programmers quickly built and ran their own fuzzers, rushed to fix the reported errors, and learned not to trust external inputs anymore.
What kind of problems did Miller's fuzzing experiment find? It turns out that the mistakes programmers made in 1990 are still the same mistakes being made today.
Buffer Overflows¶
Many programs have built-in maximum lengths for inputs and input elements. In languages like C, it is easy to excess these lengths without the program (or the programmer) even noticing, triggering so-called buffer overflows. The following code, for instance, happily copies the input string into a weekday string even if input has more than eight characters:
char weekday[9]; // 8 characters + trailing '\0' terminator
strcpy (weekday, input);
Ironically, this already fails if input is "Wednesday" (9 characters); any excess characters (here, 'y' and the following '\0' string terminator) are simply copied to whatever resides in memory after weekday, triggering arbitrary behavior; maybe some boolean character variable which would be set from 'n' to 'y'. With fuzzing, it is very easy to produce arbitrary long inputs and input elements.
We can easily simulate this buffer overflow behavior in a Python function:
def crash_if_too_long(s):
buffer = "Thursday"
if len(s) > len(buffer):
raise ValueError
And yes, it quickly crashes.
from ExpectError import ExpectError
trials = 100
with ExpectError():
for i in range(trials):
s = fuzzer()
crash_if_too_long(s)
Traceback (most recent call last):
File "/var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/ipykernel_73726/292568387.py", line 5, in <cell line: 2>
crash_if_too_long(s)
File "/var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/ipykernel_73726/2784561514.py", line 4, in crash_if_too_long
raise ValueError
ValueError (expected)
Missing Error Checks¶
Many programming languages do not have exceptions, but instead have functions return special error codes in exceptional circumstances. The C function getchar(), for instance, normally returns a character from the standard input; if no input is available anymore, it returns the special value EOF (end of file). Now assume a programmer is scanning the input for the next character, reading in characters with getchar() until a space character is read:
while (getchar() != ' ');
What happens if the input ends prematurely, as would perfectly be feasible with fuzzing? Well, getchar() returns EOF, and keeps on returning EOF when called again; so the code above simply enters an infinite loop.
Again, we can simulate such missing error checks. Here's a function that will effectively hang if no space is present in the input:
def hang_if_no_space(s):
i = 0
while True:
if i < len(s):
if s[i] == ' ':
break
i += 1
Using the timeout mechanism from our Introduction to Testing, we can interrupt this function after some time. And yes, it does hang after a few fuzzing inputs.
from ExpectError import ExpectTimeout
trials = 100
with ExpectTimeout(2):
for i in range(trials):
s = fuzzer()
hang_if_no_space(s)
Traceback (most recent call last):
File "/var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/ipykernel_73726/3194687366.py", line 5, in <cell line: 2>
hang_if_no_space(s)
File "/var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/ipykernel_73726/3035466707.py", line 4, in hang_if_no_space
if i < len(s):
File "Timeout.ipynb", line 43, in timeout_handler
raise TimeoutError()
TimeoutError (expected)
The with ExpectTimeout() line in the above code ensures that execution of the enclosed code is interrupted after two seconds, printing the error message.
Rogue Numbers¶
With fuzzing, it is easy to generate uncommon values in the input, causing all kinds of interesting behavior. Consider the following code, again in the C language, which first reads a buffer size from the input, and then allocates a buffer of the given size:
char *read_input() {
size_t size = read_buffer_size();
char *buffer = (char *)malloc(size);
// fill buffer
return (buffer);
}
What happens if size is very large, exceeding program memory? What happens if size is less than the number of characters following? What happens if size is negative? By providing a random number here, fuzzing can create all kinds of damages.
Again, we can easily simulate such rogue numbers in Python. The function collapse_if_too_large() fails if the passed value (a string) is too large after having been converted to an integer.
def collapse_if_too_large(s):
if int(s) > 1000:
raise ValueError
We can have fuzzer() create a string of digits:
long_number = fuzzer(100, ord('0'), 10)
print(long_number)
7056414967099541967374507745748918952640135045
If we feed such numbers into collapse_if_too_large(), it will very soon fail.
with ExpectError():
collapse_if_too_large(long_number)
Traceback (most recent call last):
File "/var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/ipykernel_73726/2775103647.py", line 2, in <cell line: 1>
collapse_if_too_large(long_number)
File "/var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/ipykernel_73726/1591744602.py", line 3, in collapse_if_too_large
raise ValueError
ValueError (expected)
If we really wanted to allocate that much memory on a system, having it quickly fail as above actually would be the better option. In reality, running out of memory may dramatically slow systems down, up to the point that they become totally unresponsive – and restarting is the only option.
One might argue that these are all problems of bad programming, or of bad programming languages. But then, there are thousands of people starting to program every day, and all of them make the same mistakes again and again, even today.
Catching Errors¶
When Miller and his students built their first fuzzer, they could identify errors simply because the program would crash or hang – two conditions that are easy to identify. If the failures are more subtle, though, we need to come up with additional checks.
Generic Checkers¶
Buffer overflows, as discussed above, are a particular instance of a more general problem: In languages like C and C++, a program can access arbitrary parts of its memory – even those parts that are uninitialized, already freed or simply not part of the data structure you are trying to access. This is necessary if you want to write an operating system, and great if you want a maximum of performance or control, but pretty bad if you want to avoid mistakes. Fortunately, there are tools that help catching such issues at runtime, and they are great when combined with fuzzing.
Checking Memory Accesses¶
To catch problematic memory accesses during testing, one can run C programs in special memory-checking environments; at runtime, these check for each and every memory operation whether it accesses valid and initialized memory. A popular example is LLVM Address Sanitizer which detects a whole set of potentially dangerous memory safety violations. In the following example we will compile a rather simple C program with this tool and provoke an out-of-bounds read by reading past an allocated portion of memory.
with open("program.c", "w") as f:
f.write("""
#include <stdlib.h>
#include <string.h>
int main(int argc, char** argv) {
/* Create an array with 100 bytes, initialized with 42 */
char *buf = malloc(100);
memset(buf, 42, 100);
/* Read the N-th element, with N being the first command-line argument */
int index = atoi(argv[1]);
char val = buf[index];
/* Clean up memory so we don't leak */
free(buf);
return val;
}
""")
print_file("program.c")
#include <stdlib.h> #include <string.h> int main(int argc, char** argv) { /* Create an array with 100 bytes, initialized with 42 */ char *buf = malloc(100); memset(buf, 42, 100); /* Read the N-th element, with N being the first command-line argument */ int index = atoi(argv[1]); char val = buf[index]; /* Clean up memory so we don't leak */ free(buf); return val; }
We compile this C program with address sanitization enabled:
!clang -fsanitize=address -g -o program program.c
If we run the program with an argument of 99, it returns buf[99], which is 42.
!./program 99; echo $?
program(73889,0x1fd223840) malloc: nano zone abandoned due to inability to reserve vm space. 42
Accessing buf[110], however, results in an out-of-bounds error in AddressSanitizer.
!./program 110
program(73891,0x1fd223840) malloc: nano zone abandoned due to inability to reserve vm space. ================================================================= ==73891==ERROR: AddressSanitizer: heap-buffer-overflow on address 0x60b0000000ae at pc 0x000100557e84 bp 0x00016f8aa9f0 sp 0x00016f8aa9e8 READ of size 1 at 0x60b0000000ae thread T0 #0 0x100557e80 in main program.c:12 #1 0x197d8c270 (<unknown module>) 0x60b0000000ae is located 10 bytes after 100-byte region [0x60b000000040,0x60b0000000a4) allocated by thread T0 here: #0 0x1009c4c04 in malloc+0x94 (libclang_rt.asan_osx_dynamic.dylib:arm64e+0x54c04) #1 0x100557dc8 in main program.c:7 #2 0x197d8c270 (<unknown module>) SUMMARY: AddressSanitizer: heap-buffer-overflow program.c:12 in main Shadow bytes around the buggy address: 0x60affffffe00: 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 0x60affffffe80: 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 0x60afffffff00: 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 0x60afffffff80: 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 0x60b000000000: fa fa fa fa fa fa fa fa 00 00 00 00 00 00 00 00 =>0x60b000000080: 00 00 00 00 04[fa]fa fa fa fa fa fa fa fa fa fa 0x60b000000100: fa fa fa fa fa fa fa fa fa fa fa fa fa fa fa fa 0x60b000000180: fa fa fa fa fa fa fa fa fa fa fa fa fa fa fa fa 0x60b000000200: fa fa fa fa fa fa fa fa fa fa fa fa fa fa fa fa 0x60b000000280: fa fa fa fa fa fa fa fa fa fa fa fa fa fa fa fa 0x60b000000300: fa fa fa fa fa fa fa fa fa fa fa fa fa fa fa fa Shadow byte legend (one shadow byte represents 8 application bytes): Addressable: 00 Partially addressable: 01 02 03 04 05 06 07 Heap left redzone: fa Freed heap region: fd Stack left redzone: f1 Stack mid redzone: f2 Stack right redzone: f3 Stack after return: f5 Stack use after scope: f8 Global redzone: f9 Global init order: f6 Poisoned by user: f7 Container overflow: fc Array cookie: ac Intra object redzone: bb ASan internal: fe Left alloca redzone: ca Right alloca redzone: cb ==73891==ABORTING
If you want to find errors in a C program, turning on such checks for fuzzing is fairly easy. It will slow down execution by a certain factor depending on the tool (for AddressSanitizer it is typically 2$\times$) and also consume more memory, but CPU cycles are dead cheap compared to the human effort it takes to find these bugs.
Out-of-bounds accesses to memory are a great security risk, as they may let attackers access or even modify information that is not meant for them. As a famous example, the HeartBleed bug was a security bug in the OpenSSL library, implementing cryptographic protocols that provide communications security over a computer network. (If you read this text in a browser, it is likely encrypted using these protocols.)
The HeartBleed bug was exploited by sending a specially crafted command to the SSL heartbeat service. A heartbeat service is used to check if the server on the other end is still alive. A client would send the service a string like
BIRD (4 letters)
to which the server would reply with BIRD, and the client would know the server is alive.
Unfortunately, this service could be exploited by asking the server to reply with more than the requested set of letters. This is very well explained in this XKCD comic:
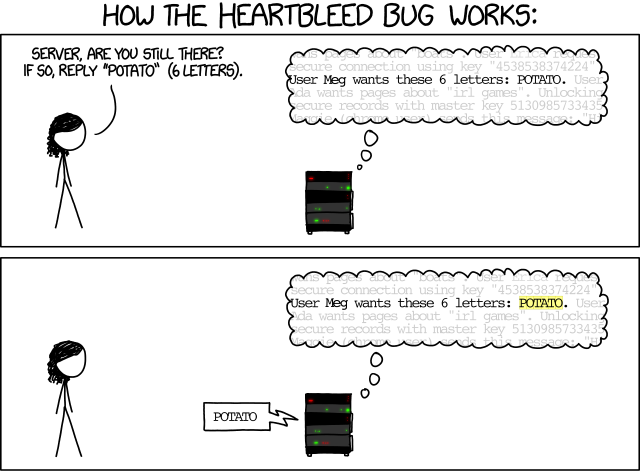
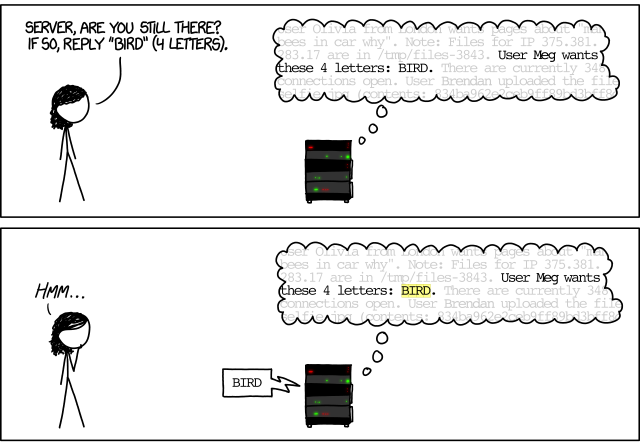
In the OpenSSL implementation, these memory contents could involve cryptographic certificates, private keys, and more – and worse, no one would notice that this memory just had been accessed. When the HeartBleed bug was discovered, it had been around for many years, and none would know whether and which secrets had already leaked; the quickly set up HeartBleed announcement page said it all.
But how was HeartBleed discovered? Very simple. Researchers both at the Codenomicon company as well as with Google compiled the OpenSSL library with a memory sanitizer, and then happily flooded it with fuzzed commands. The memory sanitizer would then notice whether an out-of-bounds memory access had occurred – and actually, it would very quickly discover this.
A memory checker is just one of many checkers one can run to detect runtime errors during fuzzing. In the chapter on mining function specifications, we will learn more about how to define generic checkers.
Information Leaks¶
Information leaks may not only occur through illegal memory accesses; they can also occur within "valid" memory – if this "valid" memory contains sensitive information that should not leak out. Let us illustrate this issue in a Python program. To start with, let us create some program memory filled with actual data and random data:
secrets = ("<space for reply>" + fuzzer(100) +
"<secret-certificate>" + fuzzer(100) +
"<secret-key>" + fuzzer(100) + "<other-secrets>")
We add more "memory" characters to secrets, filled with "deadbeef" as marker for uninitialized memory:
uninitialized_memory_marker = "deadbeef"
while len(secrets) < 2048:
secrets += uninitialized_memory_marker
We define a service (similar to the heartbeat service discussed above) that would take a reply to be sent back, as well as a length. It would store the reply to be sent in memory, and then send it back with the given length.
def heartbeat(reply: str, length: int, memory: str) -> str:
# Store reply in memory
memory = reply + memory[len(reply):]
# Send back heartbeat
s = ""
for i in range(length):
s += memory[i]
return s
This perfectly works for standard strings:
heartbeat("potato", 6, memory=secrets)
'potato'
heartbeat("bird", 4, memory=secrets)
'bird'
However, if the length is greater than the length of the reply string, additional contents of memory spill out. Note that all of this still occurs within regular array bounds, so an address sanitizer would not be triggered:
heartbeat("hat", 500, memory=secrets)
'hatace for reply>#,,!3?30>#61)$4--8=<7)4 )03/%,5+! "4)0?.9+?3();<42?=?0<secret-certificate>7(+/+((1)#/0\'4!>/<#=78%6$!!$<-"3"\'-?1?85!05629%/); *)1\'/=9%<secret-key>.(#.4%<other-secrets>deadbeefdeadbeefdeadbeefdeadbeefdeadbeefdeadbeefdeadbeefdeadbeefdeadbeefdeadbeefdeadbeefdeadbeefdeadbeefdeadbeefdeadbeefdeadbeefdeadbeefdeadbeefdeadbeefdeadbeefdeadbeefdeadbeefdeadbeefdeadbeefdeadbeefdeadbeefdeadbeefdeadbeefdeadbeefdeadbeefdeadbeefdeadbeefdeadbeefdeadbeefdeadbeefdeadbeefdeadbeefdeadbeefdeadbeefdeadb'
How can one detect such issues? The idea is to identify information that should not leak out, such as the given secrets, but also uninitialized memory. We can simulate such a check in a small Python example:
with ExpectError():
for i in range(10):
s = heartbeat(fuzzer(), random.randint(1, 500), memory=secrets)
assert not s.find(uninitialized_memory_marker)
assert not s.find("secret")
Traceback (most recent call last):
File "/var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/ipykernel_73726/4040656327.py", line 4, in <cell line: 1>
assert not s.find(uninitialized_memory_marker)
AssertionError (expected)
With such a check, we find that secrets and/or uninitialized memory indeed leak out. In the chapter on information flow, we will discuss how to do this automatically, "tainting" sensitive information and values derived from them, and ensuring that "tainted" values do not leak out.
As a rule of thumb, you should always enable as many automatic checkers as possible during fuzzing. CPU cycles are cheap, and errors are expensive. If you only execute the program without an option to actually detect errors, you will be missing several opportunities.
Program-Specific Checkers¶
Besides generic checkers that apply to all programs on a given platform or in a given language, you can also devise specific checkers that apply to your program, or a subsystem. In the chapter on testing, we already have hinted at techniques of runtime verification that check function results at runtime for correctness.
One key idea for detecting errors early is the concept of assertion – a predicate that checks the input (precondition) and the result (postcondition) of important functions. The more assertions you have in your program, the higher your chances to detect errors during execution that would go undetected by generic checkers – notably during fuzzing. If you worry about the impact of assertions on performance, keep in mind that assertions can be turned off in production code (although it can be helpful to leave the most critical checks active).
One of the most important uses of assertions for finding errors is checking the integrity of complex data structures. Let us illustrate the concept using a simple example. Suppose we have a mapping of airport codes to airports, as in
airport_codes: Dict[str, str] = {
"YVR": "Vancouver",
"JFK": "New York-JFK",
"CDG": "Paris-Charles de Gaulle",
"CAI": "Cairo",
"LED": "St. Petersburg",
"PEK": "Beijing",
"HND": "Tokyo-Haneda",
"AKL": "Auckland"
} # plus many more
airport_codes["YVR"]
'Vancouver'
"AKL" in airport_codes
True
This list of airport codes may be pretty critical: if we have a spelling mistake in any of the airport codes, this may impact whatever application we have. We therefore introduce a function that checks the list for consistency. The consistency condition is called a representation invariant, and functions (or methods) that check it are therefore typically named repOK() for "the representation is ok".
First, let's have a checker for individual airport codes. The checker fails if the code is inconsistent.
def code_repOK(code: str) -> bool:
assert len(code) == 3, "Airport code must have three characters: " + repr(code)
for c in code:
assert c.isalpha(), "Non-letter in airport code: " + repr(code)
assert c.isupper(), "Lowercase letter in airport code: " + repr(code)
return True
assert code_repOK("SEA")
We can now use code_repOK() to check all elements in the list:
def airport_codes_repOK():
for code in airport_codes:
assert code_repOK(code)
return True
with ExpectError():
assert airport_codes_repOK()
If we add an invalid element to the list, our check would fail:
airport_codes["YMML"] = "Melbourne"
with ExpectError():
assert airport_codes_repOK()
Traceback (most recent call last):
File "/var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/ipykernel_73726/2308942452.py", line 2, in <cell line: 1>
assert airport_codes_repOK()
File "/var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/ipykernel_73726/480627665.py", line 3, in airport_codes_repOK
assert code_repOK(code)
File "/var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/ipykernel_73726/865020192.py", line 2, in code_repOK
assert len(code) == 3, "Airport code must have three characters: " + repr(code)
AssertionError: Airport code must have three characters: 'YMML' (expected)
Of course, rather than manipulating the list directly, we'd have a special function for adding elements; this could then also check whether the code is valid:
def add_new_airport(code: str, city: str) -> None:
assert code_repOK(code)
airport_codes[code] = city
with ExpectError(): # For BER, ExpectTimeout would be more appropriate
add_new_airport("BER", "Berlin")
This check also allows us to find out errors in argument lists:
with ExpectError():
add_new_airport("London-Heathrow", "LHR")
Traceback (most recent call last):
File "/var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/ipykernel_73726/1427835309.py", line 2, in <cell line: 1>
add_new_airport("London-Heathrow", "LHR")
File "/var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/ipykernel_73726/2655039924.py", line 2, in add_new_airport
assert code_repOK(code)
File "/var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/ipykernel_73726/865020192.py", line 2, in code_repOK
assert len(code) == 3, "Airport code must have three characters: " + repr(code)
AssertionError: Airport code must have three characters: 'London-Heathrow' (expected)
For maximum checking, though, the add_new_airport() function would also ensure the correct representation of the list of airport codes – before and after changing it.
def add_new_airport_2(code: str, city: str) -> None:
assert code_repOK(code)
assert airport_codes_repOK()
airport_codes[code] = city
assert airport_codes_repOK()
This catches the inconsistency introduced earlier:
with ExpectError():
add_new_airport_2("IST", "Istanbul Yeni Havalimanı")
Traceback (most recent call last):
File "/var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/ipykernel_73726/1096579022.py", line 2, in <cell line: 1>
add_new_airport_2("IST", "Istanbul Yeni Havalimanı")
File "/var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/ipykernel_73726/2099116665.py", line 3, in add_new_airport_2
assert airport_codes_repOK()
File "/var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/ipykernel_73726/480627665.py", line 3, in airport_codes_repOK
assert code_repOK(code)
File "/var/folders/n2/xd9445p97rb3xh7m1dfx8_4h0006ts/T/ipykernel_73726/865020192.py", line 2, in code_repOK
assert len(code) == 3, "Airport code must have three characters: " + repr(code)
AssertionError: Airport code must have three characters: 'YMML' (expected)
The more repOK() assertions exist in your code, the more errors you will catch – even those specific to only your domain and problem. On top, such assertions document the assumptions you made during programming and thus help other programmers to understand your code and prevent errors.
As a final example, let us consider a rather complex data structure – a red-black tree, a self-balancing binary search tree. Implementing a red-black tree is not too hard, but getting it correct can be a task of several hours even for experienced programmers. A repOK() method, however, documents all the assumptions and checks them as well:
class RedBlackTree:
def repOK(self):
assert self.rootHasNoParent()
assert self.rootIsBlack()
assert self.rootNodesHaveOnlyBlackChildren()
assert self.treeIsAcyclic()
assert self.parentsAreConsistent()
return True
def rootIsBlack(self):
if self.parent is None:
assert self.color == BLACK
return True
def add_element(self, elem):
assert self.repOK()
... # Add the element
assert self.repOK()
def delete_element(self, elem):
assert self.repOK()
... # Delete the element
assert self.repOK()
Here, repOK() is a method that runs on an object of the RedBlackTree class. It runs five different checks, all of which have their own assertions. Whenever an element is added or deleted, all these consistency checks are run automatically. If you have an error in any of these, the checkers will find them – if you run the tree through sufficiently many fuzzed inputs, of course.
typed_airport_codes: Dict[str, str] = {
"YVR": "Vancouver", # etc
}
If we now add a key with a non-string type, as in
typed_airport_codes[1] = "First" # type: ignore
this would be caught by MyPy immediately:
$ mypy airports.py
airports.py: error: Invalid index type "int" for "Dict[str, str]"; expected type "str"
Statically checking more advanced properties such as the airport code consisting of exactly three uppercase characters or a tree being acyclic, however, quickly reach the limits of static checking. Your repOK() assertions will still be needed – best in conjunction with a good test generator.
A Fuzzing Architecture¶
Since we'd like to reuse some parts of this chapter in the following ones, let us define things in a way that are easier to reuse, and in particular easier to extend. To this end, we introduce a number of classes that encapsulate the functionality above in a reusable way.
Runner Classes¶
The first thing we introduce is the notion of a Runner – that is, an object whose job it is to execute some object with a given input. A runner typically is some program or function under test, but we can also have simpler runners.
Let us start with a base class for runners. A runner essentially provides a method run(input) that is used to pass input (a string) to the runner. run() returns a pair (result, outcome). Here, result is a runner-specific value that gives details on the run; outcome is a value that classifies the result in three categories:
Runner.PASS– the test passed. The run produced correct results.Runner.FAIL– the test failed. The run produced incorrect results.Runner.UNRESOLVED– the test neither passed nor failed. This happens if the run could not take place – for instance, because the input was invalid.
Outcome = str
class Runner:
"""Base class for testing inputs."""
# Test outcomes
PASS = "PASS"
FAIL = "FAIL"
UNRESOLVED = "UNRESOLVED"
def __init__(self) -> None:
"""Initialize"""
pass
def run(self, inp: str) -> Any:
"""Run the runner with the given input"""
return (inp, Runner.UNRESOLVED)
As a base class, Runner merely provides an interface for more complex runners that build on it. More specifically, we introduce subclasses that inherit the methods from their superclass in order to add additional methods or to override inherited methods.
Here is one example of such a subclass: PrintRunner simply prints out everything that is given to it, overriding the inherited run() method. This is the default runner in many situations.
class PrintRunner(Runner):
"""Simple runner, printing the input."""
def run(self, inp) -> Any:
"""Print the given input"""
print(inp)
return (inp, Runner.UNRESOLVED)
p = PrintRunner()
(result, outcome) = p.run("Some input")
Some input
The result is just the string we passed as input:
result
'Some input'
Still, at this point, we have no way to classify program behavior:
outcome
'UNRESOLVED'
The ProgramRunner class sends the input to the standard input of a program instead. The program is specified when creating a ProgramRunner object.
class ProgramRunner(Runner):
"""Test a program with inputs."""
def __init__(self, program: Union[str, List[str]]) -> None:
"""Initialize.
`program` is a program spec as passed to `subprocess.run()`"""
self.program = program
def run_process(self, inp: str = "") -> subprocess.CompletedProcess:
"""Run the program with `inp` as input.
Return result of `subprocess.run()`."""
return subprocess.run(self.program,
input=inp,
stdout=subprocess.PIPE,
stderr=subprocess.PIPE,
universal_newlines=True)
def run(self, inp: str = "") -> Tuple[subprocess.CompletedProcess, Outcome]:
"""Run the program with `inp` as input.
Return test outcome based on result of `subprocess.run()`."""
result = self.run_process(inp)
if result.returncode == 0:
outcome = self.PASS
elif result.returncode < 0:
outcome = self.FAIL
else:
outcome = self.UNRESOLVED
return (result, outcome)
Here's a variant for binary (i.e., non-textual) input and output.
class BinaryProgramRunner(ProgramRunner):
def run_process(self, inp: str = "") -> subprocess.CompletedProcess:
"""Run the program with `inp` as input.
Return result of `subprocess.run()`."""
return subprocess.run(self.program,
input=inp.encode(),
stdout=subprocess.PIPE,
stderr=subprocess.PIPE)
Let us demonstrate a ProgramRunner using the cat program – a program that copies its input to its output. We see that a standard invocation of cat simply does the job, with the output of cat being the same as its input:
cat = ProgramRunner(program="cat")
cat.run("hello")
(CompletedProcess(args='cat', returncode=0, stdout='hello', stderr=''), 'PASS')
Fuzzer Classes¶
Let us now define a fuzzer that actually feed data into a consumer. The base class for fuzzers provides one central method fuzz() that creates some input. The run() function then sends the fuzz() input to a runner, returning the outcome; runs() does this for a given number (trials) of times.
class Fuzzer:
"""Base class for fuzzers."""
def __init__(self) -> None:
"""Constructor"""
pass
def fuzz(self) -> str:
"""Return fuzz input"""
return ""
def run(self, runner: Runner = Runner()) \
-> Tuple[subprocess.CompletedProcess, Outcome]:
"""Run `runner` with fuzz input"""
return runner.run(self.fuzz())
def runs(self, runner: Runner = PrintRunner(), trials: int = 10) \
-> List[Tuple[subprocess.CompletedProcess, Outcome]]:
"""Run `runner` with fuzz input, `trials` times"""
return [self.run(runner) for i in range(trials)]
By default, Fuzzer objects do not do much, as their fuzz() function is merely an abstract placeholder. The subclass RandomFuzzer, however, implements the functionality of the fuzzer() function, above, adding a parameter min_length to specify a minimum length.
class RandomFuzzer(Fuzzer):
"""Produce random inputs."""
def __init__(self, min_length: int = 10, max_length: int = 100,
char_start: int = 32, char_range: int = 32) -> None:
"""Produce strings of `min_length` to `max_length` characters
in the range [`char_start`, `char_start` + `char_range`)"""
self.min_length = min_length
self.max_length = max_length
self.char_start = char_start
self.char_range = char_range
def fuzz(self) -> str:
string_length = random.randrange(self.min_length, self.max_length + 1)
out = ""
for i in range(0, string_length):
out += chr(random.randrange(self.char_start,
self.char_start + self.char_range))
return out
With RandomFuzzer, we can now create a fuzzer whose configuration needs to be specified only once when creating the fuzzer.
random_fuzzer = RandomFuzzer(min_length=20, max_length=20)
for i in range(10):
print(random_fuzzer.fuzz())
'>23>33)(&"09.377.*3
*+:5 ? (?1$4<>!?3>.'
4+3/(3 (0%!>!(+9%,#$
/51$2964>;)2417<9"2&
907.. !7:&--"=$7',7*
(5=5'.!*+&>")6%9)=,/
?:&5) ";.0!=6>3+>)=,
6&,?:!#2))- ?:)=63'-
,)9#839%)?&(0<6("*;)
4?!(49+8=-'&499%?< '
We can now send such generated inputs to our previously defined cat runner, verifying that cat actually does copy its (fuzzed) input to its output.
for i in range(10):
inp = random_fuzzer.fuzz()
result, outcome = cat.run(inp)
assert result.stdout == inp
assert outcome == Runner.PASS
Combining a Fuzzer with a Runner, however, is so common that we can use the run() method supplied by the Fuzzer class for this purpose:
random_fuzzer.run(cat)
(CompletedProcess(args='cat', returncode=0, stdout='?:+= % <1<6$:(>=:9)5', stderr=''), 'PASS')
With runs(), we can repeat a fuzzing run a number of times, obtaining a list of results.
random_fuzzer.runs(cat, 10)
[(CompletedProcess(args='cat', returncode=0, stdout='3976%%&+%6=(1)3&3:<9', stderr=''), 'PASS'), (CompletedProcess(args='cat', returncode=0, stdout='33$#42$ 11=*%$20=<.-', stderr=''), 'PASS'), (CompletedProcess(args='cat', returncode=0, stdout='"?<\'#8 </:*%9.--\'97!', stderr=''), 'PASS'), (CompletedProcess(args='cat', returncode=0, stdout="/0-#(03/!#60'+6>&&72", stderr=''), 'PASS'), (CompletedProcess(args='cat', returncode=0, stdout="=,+:,6'5:950+><3(*()", stderr=''), 'PASS'), (CompletedProcess(args='cat', returncode=0, stdout=" 379+0?'%3137=2:4605", stderr=''), 'PASS'), (CompletedProcess(args='cat', returncode=0, stdout="02>!$</'*81.#</22>+:", stderr=''), 'PASS'), (CompletedProcess(args='cat', returncode=0, stdout="=-<'3-#88*%&*9< +1&&", stderr=''), 'PASS'), (CompletedProcess(args='cat', returncode=0, stdout='2;;0=3&6=8&30&<-;?*;', stderr=''), 'PASS'), (CompletedProcess(args='cat', returncode=0, stdout='/#05=*3($>::#7!0=12+', stderr=''), 'PASS')]
With this, we have all in place to create fuzzers – starting with the simple random fuzzers introduced in this chapter, but even far more advanced ones. Stay tuned!
Synopsis¶
This chapter provides two important classes, introduced in A Fuzzing Architecture:
Fuzzeras a base class for fuzzers; andRunneras a base class for programs under test.
Fuzzers¶
Fuzzer is a base class for fuzzers, with RandomFuzzer as a simple instantiation. The fuzz() method of Fuzzer objects returns a string with a generated input.
random_fuzzer = RandomFuzzer()
random_fuzzer.fuzz()
'%$<1&<%+=!"83?+)9:++9138 42/ "7;0-,)06 "1(2;6>?99$%7!!*#96=>2&-/(5*)=$;0$$+;<12"?30&'
The RandomFuzzer() constructor allows a number of keyword arguments:
print(RandomFuzzer.__init__.__doc__)
Produce strings of `min_length` to `max_length` characters
in the range [`char_start`, `char_start` + `char_range`)
random_fuzzer = RandomFuzzer(min_length=10, max_length=20, char_start=65, char_range=26)
random_fuzzer.fuzz()
'XGZVDDPZOOW'
# ignore
from ClassDiagram import display_class_hierarchy
# ignore
display_class_hierarchy(RandomFuzzer,
public_methods=[
Fuzzer.__init__,
Fuzzer.fuzz,
Fuzzer.run,
Fuzzer.runs,
RandomFuzzer.fuzz,
RandomFuzzer.__init__,
],
project='fuzzingbook')
Runners¶
A Fuzzer can be paired with a Runner, which takes the fuzzed strings as input. Its result is a class-specific status and an outcome (PASS, FAIL, or UNRESOLVED). A PrintRunner will simply print out the given input and return a PASS outcome:
print_runner = PrintRunner()
random_fuzzer.run(print_runner)
EQYGAXPTVPJGTYHXFJ
('EQYGAXPTVPJGTYHXFJ', 'UNRESOLVED')
A ProgramRunner will feed the generated input into an external program. Its result is a pair of the program status (a CompletedProcess instance) and an outcome (PASS, FAIL, or UNRESOLVED):
cat = ProgramRunner('cat')
random_fuzzer.run(cat)
(CompletedProcess(args='cat', returncode=0, stdout='BZOQTXFBTEOVYX', stderr=''), 'PASS')
# ignore
display_class_hierarchy([ProgramRunner, PrintRunner],
public_methods=[
Runner.__init__,
Runner.run,
ProgramRunner.__init__,
ProgramRunner.run,
PrintRunner.run
],
project='fuzzingbook')
Lessons Learned¶
- Randomly generating inputs ("fuzzing") is a simple, cost-effective way to quickly test arbitrary programs for their robustness.
- Bugs fuzzers find are mainly due to errors and deficiencies in input processing.
- To catch errors, have as many consistency checkers as possible.
Background¶
Books on generating software tests in general are scarce (which is why we wrote this book). There are a few notable books on fuzzing, though, also based on the basic fuzzing techniques introduced in this chapter:
The book "Fuzzing – Brute Force Vulnerability Discovery" covers a wide range of fuzzing domains, including files, Web pages, environment variables, and network protocols. The authors bring in lots of experience from fuzzing at Microsoft, and include a number of ready-made tools for Windows and UNIX programs. The tools have aged somewhat, but the principles remain.
The book "Fuzzing for Software Security Testing and Quality Assurance" \cite{Takanen2008}, now in its second edition 2018, covers a wide range of fuzzing tools and detection techniques; its authors bring in plenty of experience from security testing and vulnerability discovery. This is arguably one of the most comprehensive and up-to-date books on the field.
Specifically for this chapter, the seminal work on fuzzing, introducing both the term and the approach, is "An Empirical Study of the Reliability of UNIX Utilities" \cite{Miller1990}. As the foundation for the field, this is a must-read for anyone interested in fuzzing and robustness testing, with observations as valid today as they were 30 years ago.
Exercises¶
One of the errors found by Miller et al. \cite{Miller1990} involves the troff typesetting system. Troff takes as input a text consisting of lines; a line beginning with a dot (.) includes typesetting commands, as in
.NH
Some Heading
.LP
Some paragraph
which would produce (using nroff -ms) the text
1. Some Heading
Some paragraph
At the time of Miller et al., troff would fail if its input included
- The input sequence
\D(backslash + D) followed by a non-printable character - A character in the ASCII range 128–255 (i.e., the 8th bit is set) followed by a newline character
- A single dot (
.) followed by a newline character.
Exercise 1: Simulate Troff¶
For each of the above, write a Python function f(s) that fails if s fulfills the failure criterion.
Exercise 2: Run Simulated Troff¶
Create a class TroffRunner as subclass of Runner that checks for the above predicates. Run it with Fuzzer. Be sure to have the Fuzzer object produce the entire range of characters. Count how frequently the individual predicates fail.
Exercise 3: Run Real Troff¶
Using BinaryProgramRunner, apply the fuzzer you configured on the real troff program. Check if you can produce any run whose output code is non-zero, indicating a failure or a crash.